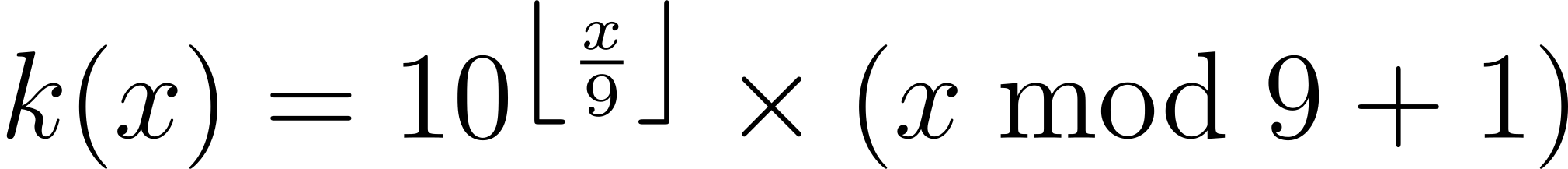1
x = 0; y = 1x100
The Kohlhas sequence visualized
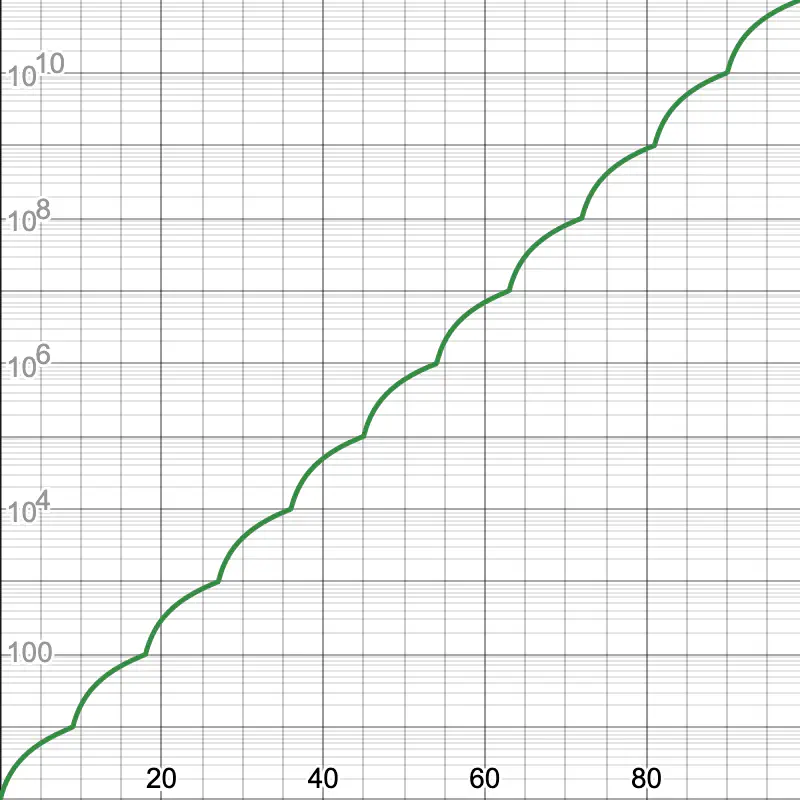
Approximating the Kohlhas sequence
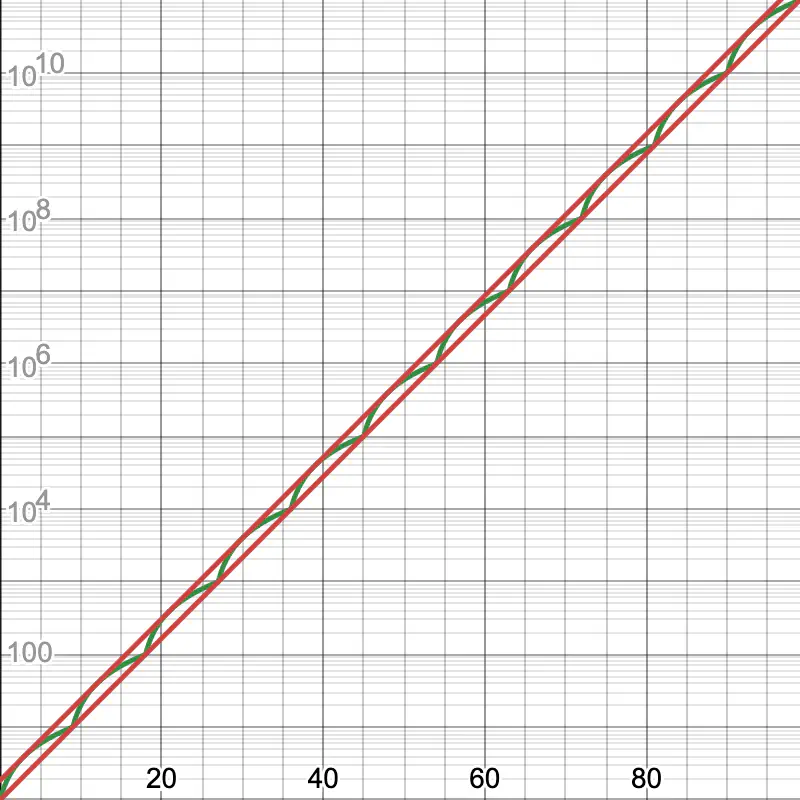
I am not sure where the magic number \(1.857134893345984732049361…\) comes from. For now I will call it the Felix constant (\(F\)).
I have found where the constant comes from, but have lost it when my browser recently crashed. I will try to recover my findings…
Generating the Kohlhas sequence
def kohlhas_sequence(x):
return 10 ** (x // 9) * (x % 9 + 1)
Examples of the Kohlhas sequence
Here are the first 99 numbers of the Kohlhas sequence:
1
2
3
4
5
6
7
8
9
10
20
30
40
50
60
70
80
90
100
200
300
400
500
600
700
800
900
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
20000
30000
40000
50000
60000
70000
80000
90000
100000
200000
300000
400000
500000
600000
700000
800000
900000
1000000
2000000
3000000
4000000
5000000
6000000
7000000
8000000
9000000
10000000
20000000
30000000
40000000
50000000
60000000
70000000
80000000
90000000
100000000
200000000
300000000
400000000
500000000
600000000
700000000
800000000
900000000
1000000000
2000000000
3000000000
4000000000
5000000000
6000000000
7000000000
8000000000
9000000000
10000000000
20000000000
30000000000
40000000000
50000000000
60000000000
70000000000
80000000000
90000000000
100000000000
Number of digits at \(k(x)\)
def kohlhas_ndigits(x):
return x // 9 + 1
Related sequences
$$ \text{ohlhas\_sequence} \equiv 10^{\left\lfloor \frac{x}{18} \right\rfloor} \times (x \bmod 18 + 2) \\ $$def ohlhas_sequence(x):
return 10 ** (x // 18) * (x % 18 + 2)
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900
def hlhas_sequence(x):
return 10 ** (x // 27) * (x % 27 + 3)
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290
…